Uniform Spaces 3 - The Completion of a Uniform Space

Pre-requisites: point-set topology, metric spaces, familiarity with commutative diagrams, previous posts on uniform spaces.

This is the third post in my series on uniform spaces. See my other posts here:

1. Nets
2. Introduction to Uniform Spaces
3. The Completion of a Uniform Space
4. The Bolzano-Weierstrass Theorem
5. Countably Uniform Spaces

Cauchy Nets

In a metric space, a sequence $a_\bullet$ is said to be Cauchy if for any $\epsilon > 0$, there exists $N \in \mathbb{N}$ such that $d(a_n, a_m) < \epsilon$ for all $n, m \geq N$. In other words, a sequence is Cauchy if the distance between terms becomes arbitrarily small. This looks very similar to the definition of a convergent sequence in a metric space, and indeed every convergent sequence is Cauchy, but a Cauchy sequence need not converge to any point. In many situations, things become much simpler if every Cauchy sequence does converge to a point. Such a metric space is called a complete metric space. There is also a canonical way to enlarge a metric space by essentially adding a limit point for each Cauchy sequence. This construction is called the completion of a metric space. I won't go over this construction here, but it is the motivation for much of this blog post.

These ideas can all be brought over into the world of separated uniform spaces, replacing convergence of sequence with convergence of nets, and replacing Cauchy sequences with Cauchy nets. In this section, we will only deal with separated uniform spaces because non-separated uniform spaces do not have unique limits.

Definition: A net $a_\bullet$ in a separated uniform space $(X, \Phi)$ is said to be Cauchy if for all entourages $A \in \Phi$, eventually $(a_\bullet, a_\bullet) \in A$.

By this, we mean that there exists an index $i$ such that for all $j, k > i$, $(a_j, a_k) \in A$. The indices on each $a_\bullet$ need not be the same.

Just as in metric spaces, convergent nets are always Cauchy.

Lemma (Convergent Implies Cauchy): Let $(X, \Phi)$ be a separated uniform space, and let $a_\bullet$ net in $X$ that converges. Then, $a_\bullet$ is Cauchy.

Proof: Suppose that $a_\bullet$ converges to $x$. Fix $A \in \Phi$. Let $B \in \Phi$ be a symmetric entourage such that $B \circ B \subset A$. Since $(a_\bullet, x) \in B$ eventually, $(a_\bullet, a_\bullet) \in A$ eventually. $\square$.

However, Cauchy nets are not always convergent. For an example, take any incomplete metric space (as a uniform space).

The Completion of a Uniform Space

Definition: A separated uniform space is complete if every Cauchy net converges.

Complete uniform spaces are much nicer to work with than arbitrary uniform spaces because every point that you want to work with actually exists. For example, in the next post, I will go over a proof that a complete uniform space is compact if and only if it is totally bounded (which generalizes a familiar theorem for metric spaces). Although it is outside the scope of these notes, you can sometimes do calculus with uniform spaces (specifically locally convex vector spaces), but this gets very complicated if the uniform space is not complete.

In many cases, separated uniform spaces can be replaced by complete uniform spaces without any problems. This operation of turning a separated uniform space into a complete uniform space is called the completion.

Theorem (The Completion): Let $X$ be a separated uniform space. There exists a complete uniform space $\overline{X}$ and a uniform embedding $\iota_X: X \rightarrow \overline{X}$ such that whenever $Y$ is a complete uniform space and $f: X \rightarrow Y$ is a uniform function, then $f$ factors uniquely through $\iota_X$ as in the following commutative diagram. We will call this the universal property of the completion. Moreover, $\overline{X}$ is unique up to uniform isomorphism.

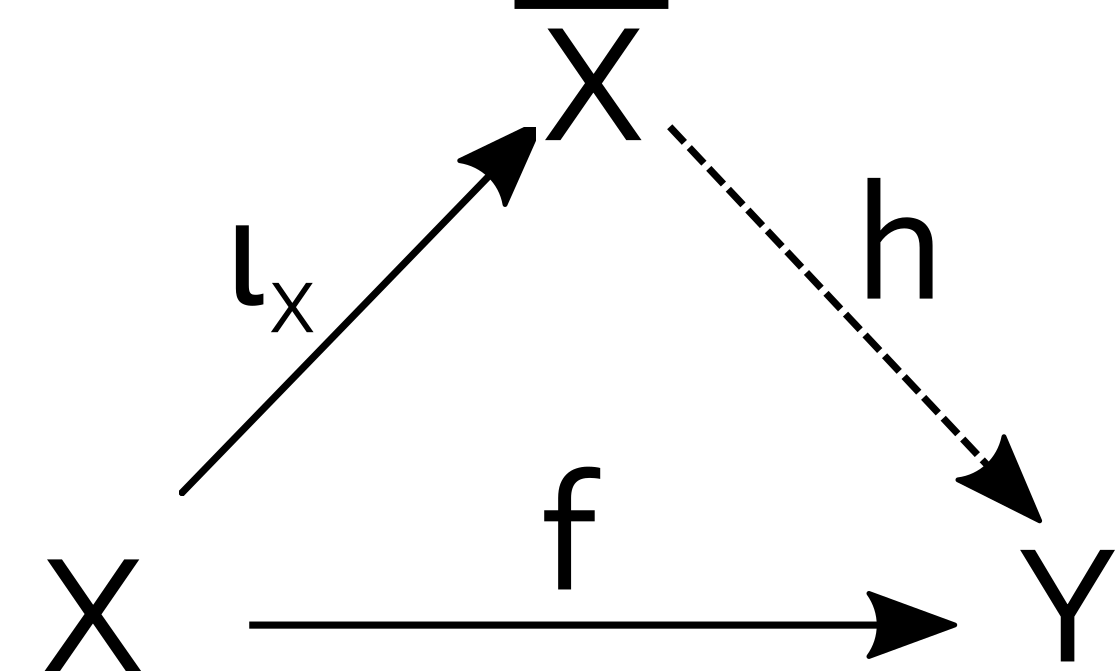
The proof is bogged down by technicalities and a bit long to put here. For a full proof, see this paper by Bhowmik Subrata (which uses filters instead of nets). The basic construction is as follows.

Define $Y$ to be the set of all Cauchy nets in $X$. Define two Cauchy sequences to be co-Cauchy if for any entourage $A$ of $X$, eventually $(a_\bullet, b_\bullet) \in A$. Co-Cauchiness is an equivalence relation on $Y$, and the quotient of $Y$ by this equivalence relation is a complete uniform space, which we call $\overline{X}$. Define $\iota_X: X \rightarrow \overline{X}$ by: $\iota_X(x)$ is the equivalence class of all that nets that converge to $x$. It can be shown that $\overline{X}$ and $\iota_X$ satisfy the conditions of the above theorem.

In particular, let $f: X \rightarrow Y$ be any uniform function. Then, $\iota_Y \circ f: X \rightarrow \overline{Y}$, so $\iota_Y \circ f$ factors uniquely through $\iota_X$ as in the following commutative diagram.

Thus, every uniform function $f: X \rightarrow Y$ extends uniquely to a function $\overline{f}: \overline{X} \rightarrow \overline{Y}$.

Dense Embeddings

The universal property of the completion may be a little abstract, especially to people not familiar with category theory. We can make the completion a bit more concrete with the language of dense embeddings. Recall that a subset $A$ of a topological space $X$ is dense if the closure of $A$ is all of $X$. We call a continuous function $f: X \rightarrow Y$ dense if its image is dense in $Y$. In the same way that embeddings correspond to subspaces, dense embeddings correspond to dense subspaces.

The dense subspaces of a topological space $X$ carry a lot of information about $X$ itself. For example, if $A$ is a dense subspace of $X$, and $f, g: X \rightarrow Y$ are two continuous functions, then $f$ and $g$ are equal if and only if they are equal on $A$. I like to think of a dense subspace of a space $X$ as a skeletal outline of $X$. On the other hand, I like to think of a dense embedding of $A$ as a way to enlarge $A$.

How a fixed space can be enlarged is an important question, with answers depending on the context. A compactification of a topological space is a dense embedding into a compact (Hausdorff) topological space. Assuming the Axiom of Choice, the Stone–Čech compactification is the maximal way to compactify a (Tychonoff) topological space. Similarly, the completion of a uniform space is the maximal way to enlarge something in the context of uniform spaces.

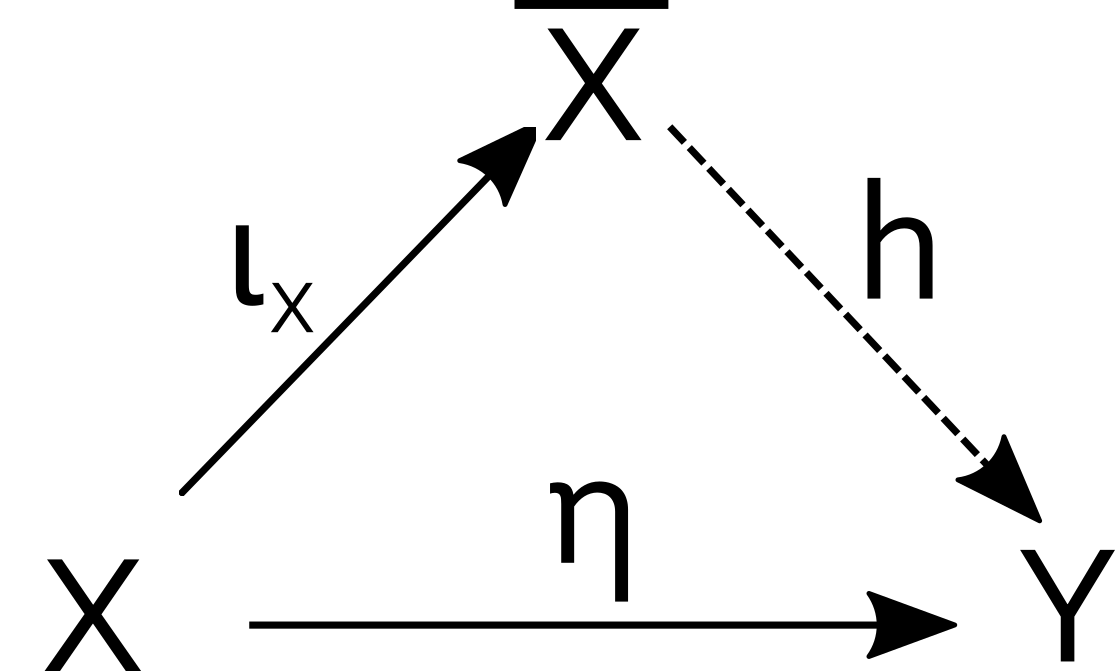
Theorem (Dense Uniform Embeddings): Let $X$ be a separated uniform space. The natural map $\iota_X: X \rightarrow \overline{X}$ is a dense uniform embedding. If $Y$ is a separated uniform space and $\eta: X \rightarrow Y$ is a dense uniform embedding, then $\eta$ uniquely factors through $\iota_X$ as in the following commutative diagram.

Completions and Functions

Complete uniform spaces are simply better than incomplete uniform spaces. Because of this, we will want to replace all incomplete uniform spaces by their completions. To do this, we often need to know when a function $X \rightarrow Y$ can be replaced by a function $\overline{X} \rightarrow \overline{Y}$ and vice versa.

In topological spaces, we have the following situation.

Theorem (Uniqueness of Extensions): Suppose that $X$ and $Z$ are topological spaces, and $Z$ is Hausdorff. Let $f: X \rightarrow Z$ be a continuous function, and suppose that $X$ is a dense subset of $Y$. Then, there is at most one continuous extension $g: Y \rightarrow Z$ of $f$.

Let $f: X \rightarrow Y$ be a continuous map of separated uniform spaces. Since $Y$ embeds into $\overline{Y}$, $f$ naturally extends to a map $X \rightarrow \overline{Y}$. Since $X$ embeds densely into $\overline{X}$, this theorem proves that there exists at most one continuous extension $g: \overline{X} \rightarrow \overline{Y}$.

Such an extension does not always exist. For example, consider the continuous map $f: (0,1) \cup (1,2) \rightarrow (0,1) \cup (2, 3)$ defined by:

Give $(0,1) \cup (1,2)$ and $(0,1) \cup (2,3)$ uniform structures as subspaces of $\mathbb{R}$. Note that $f$ is continuous but not uniformly continuous. $f$ clearly has no continuous extension $g: [0, 2] \rightarrow [0, 1] \cup [2,3]$

The correct condition to extend a continuous function to the completion is that it send Cauchy nets to Cauchy nets.

Theorem (Completion of a Continuous Function): Let $f: X \rightarrow Y$ be a continuous function. $f$ extends to a continuous function $g: \overline{X} \rightarrow \overline{Y}$ if and only if $f$ preserves Cauchy nets. If so, then $g$ is unique.

Categorical Properties of the Completion

We know that any uniform function $f: X \rightarrow Y$ has a unique uniform extension $\overline{f}: \overline{X} \rightarrow \overline{Y}$. It is straightforward to show that the association $X \mapsto \overline{X}$ and $f \mapsto \overline{f}$ actually defines a functor from the category of (separated) uniform spaces to the category of complete uniform spaces. Fundamentally, when we talk about replacing spaces by their completions, we really mean applying this functor.

The completion functor preserves products and coproducts, as shown in the following two lemmas.

Lemma: Let $(X_\alpha)_{\alpha \in I}$ be uniform spaces. Then, $\overline{\prod_{\alpha \in I} X_\alpha} \cong \prod_{\alpha \in I} \overline{X_\alpha}$ naturally. If each $X_\alpha$ is complete, then so is $\prod_{\alpha \in I} X_\alpha$.

Lemma: Let $(X_\alpha)_{\alpha \in I}$ be uniform spaces. Then, $\overline{\coprod_{\alpha \in I} X_\alpha} \cong \coprod_{\alpha \in I} \overline{X_\alpha}$ naturally. If each $X_\alpha$ is complete, then so is $\coprod_{\alpha \in I} X_\alpha$.

Even better, the completion functor commutes with arbitrary limits and colimits of (separated) uniform spaces. Proving these facts would take us too far afield, but they serve to justify why complete uniform spaces are just the best.

Extensions: It is possible to define Cauchy nets, completeness, and completions in other, more general spaces called Cauchy spaces, but these see less use than uniform spaces. Sometimes, it suffices to only consider specific classes of nets, leading to different notions of completeness and completions. A sequentially complete uniform space is one such that every Cauchy sequence converges, but larger Cauchy nets may not.